Generating set and span
Consider a vector space $\mathbb{V}=(V,+,\cdot)$ and set of vectors $A=\{x_1,\ldots,x_k\} \subseteq V$. If every vector $v \in V$ can be expressed as a linear combination of $x_1,\ldots,x_k$,$A$ is called a generating set of $V$.The set of all linear combination of vectors in $A$ is called the span of $A$.If $A$ spans the vector space $V$, we write $V=span[A]$ or $V=span[x_1,\ldots,x_k]$.
Generating sets are sets of vectors that span vector (sub)spaces, i.e.,every vector can be represented as a linear combination of the vectors in the generating set. Now, we will be more specific and characterize the smallest generating set that spans a vector (sub)space.
Basis
Consider a vector space $\mathbb{V}=(V,+,\cdot)$ and $A \subseteq V$. A generating set $A$of $V$ is called minimal if there exists no smaller set $\hat{A} \subseteq A \subseteq V$ that spans $V$.Every linearly independent generating set of $V$ is minimal and is called the basis of $V$.
Let $\mathbb{V}=(V,+,\cdot)$ be a vector space and $B \subseteq V, B \ne \phi$. Then the following statements are equivalent.
- $B$ is a basis of $V$.
- $B$ is a minimal generating set.
- $B$ is a maximal linearly independent set of vectors in $V$ ,i.e; adding any other vector to this set will make it linearly dependent.
- every vector $x \in V $ is a linear combination of vectors from $B$, and every linear combination is unique i.e, with
$x=\sum_{i=1}^{k} \lambda_ib_i= \sum_{i=1}^{k} \psi_ib_i$
and $\lambda_i,\psi_i \in \mathbb{R}, b_i \in B$ it follows that $\lambda_i=\psi_i,i=1,\ldots,k$.
Example:
In $\mathbb{R}^2$ the canonical standard basis are
Remark. Every vector space V possesses a basis B. The preceding examples show that there can be many bases of a vector space V , i.e., there is no unique basis. However, all bases possess the same number of elements,the basis vectors.
We only consider finite-dimensional vector spaces V . In this case, the dimension of V is the number of basis vectors of V , and we write dim(V ).
If $U \subseteq V $ is a subspace of V , then $dim(U) \le dim(V )$ and $dim(U) =dim(V)$ if and only if $U=V$.Intuitively, the dimension of a vector space can be thought of as the number of independent directions in this vector space.
by executing the following steps:
1. Write the spanning vectors as columns of a matrix A
2. Determine the row-echelon form of A.
3. The spanning vectors associated with the pivot columns are a basis of U.
Example:
Since the pivot columns indicate which set of vectors is linearly independent,we see from the row-echelon form that $x_1, x_2,x_4$ are linearly independent.Therefore $\{x_1,x_2,x_4\}$ is a basis of $U$.
import sympy as sp
import numpy as np
row1=[1,2,3,-1]
row2=[2,-1,-4,8]
row3=[-1,1,3,-5]
row4=[-1,2,5,-6]
row5=[-1,-2,-3,1]
M = sp.Matrix((row1,row2,row3,row4,row5))
print("Coefficient Matrix")
display(M)
print(" Echelon Form")
display(M.echelon_form())
O/P
Coefficient Matrix
$\displaystyle \left[\begin{matrix}1 & 2 & 3 & -1\\2 & -1 & -4 & 8\\-1 & 1 & 3 & -5\\-1 & 2 & 5 & -6\\-1 & -2 & -3 & 1\end{matrix}\right]$
Echelon Form
$\displaystyle \left[\begin{matrix}1 & 2 & 3 & -1\\0 & -5 & -10 & 10\\0 & 0 & 0 & -5\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{matrix}\right]$A set of $n$ linearly independent vectors in $\mathbb{R}^n$ forms a basis. Does the set of vectors $(2, 4,−3),(0, 1, 1),(0, 1,−1)$ form a basis for $\mathbb{R}^3$? Explain your reasons.
Lets find out whether these vectors form a linear independent set
2 & 0 & 0\\
4 &1 & 1\\
-3 & 1 & -1
\end{bmatrix}$
$R_1=R_1/2$
$\begin{bmatrix}
1 & 0 & 0\\
4 &1 & 1\\
-3 & 1 & -1
\end{bmatrix}$
$\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 1\\
0 & 1 & -1
\end{bmatrix}$
$\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 1\\
0 & 0 & 1
\end{bmatrix}$
$R_2=R_2-R_3$
$\begin{bmatrix}1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}$
It is noted that the three vectors are linearly independent and hence form the basis in $\mathbb{R}^3$
Determine the basis for a vector space $U \subseteq R^3$ spanned by the vectors (university question)
$x1=\begin{bmatrix}1\\
0\\
1
\end{bmatrix} x2= \begin{bmatrix}
-1\\
2\\
1\end{bmatrix}x3=\begin{bmatrix}
0\\
1\\
1\end{bmatrix}$
Represent these vectors as column of a matrix and perform row reduction. The pivot columns indicate linearly independent vectors and they form the basis of the vector space.
$\begin{bmatrix}
1 & -1 & 0\\
0 & 2 & 1\\
1 & 1 & 1
\end{bmatrix}$
1 & -1 & 0\\
0 & 2 & 1\\
1 & 1 & 1
\end{bmatrix}$
$R3=R3-R1$
$\begin{bmatrix}
1 & -1 & 0\\
0 & 2 & 1\\
0 & 2 & 1
\end{bmatrix}$
1 & -1 & 0\\
0 & 2 & 1\\
0 & 2 & 1
\end{bmatrix}$
$R3=R3-R2$
$\begin{bmatrix}
1 & -1 & 0\\
0 & 2 & 1\\
0 & 0 & 0
\end{bmatrix}$
1 & -1 & 0\\
0 & 2 & 1\\
0 & 0 & 0
\end{bmatrix}$
$R1=R1+R2$
$\begin{bmatrix}
1 & 1 & 1\\
0 & 2 & 1\\
0 & 0 & 0
\end{bmatrix}$
1 & 1 & 1\\
0 & 2 & 1\\
0 & 0 & 0
\end{bmatrix}$
$R2=R2/2$
$\begin{bmatrix}
1 & 1 & 1\\
0 & 1 & 1/2\\
0 & 0 & 0
\end{bmatrix}$
1 & 1 & 1\\
0 & 1 & 1/2\\
0 & 0 & 0
\end{bmatrix}$
$R1=R1-R2$
$\begin{bmatrix}
1 & 0 & 1/2\\
0 & 1 & 1/2\\
0 & 0 & 0
\end{bmatrix}$
It is notes that the first two columns are the pivot columns. The third vector can be represented as the linear combination of the first two vectors. So the basis is1 & 0 & 1/2\\
0 & 1 & 1/2\\
0 & 0 & 0
\end{bmatrix}$
$Basis=\begin{bmatrix}
1\\
0\\
1
\end{bmatrix} \begin{bmatrix}
-1\\
2\\
1\end{bmatrix}$
1\\
0\\
1
\end{bmatrix} \begin{bmatrix}
-1\\
2\\
1\end{bmatrix}$
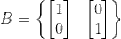


Comments
Post a Comment