5.1 Optimization using Gradient Descent

Since machine learning algorithms are implemented on a computer, the mathematical formulations are expressed as numerical optimization methods.Training a machine learning model often boils down to finding a good set of parameters. The notion of “good” is determined by the objective function or the probabilistic model. Given an objective function, finding the best value is done using optimization algorithms.

There are two main branches of continuous optimization constrained and unconstrained.

By convention, most objective functions in machine learning are intended to be minimized, that is, the best value is the minimum value. Intuitively finding the best value is like finding the valleys of the objective function, and the gradients point us uphill. The idea is to move downhill (opposite to the gradient) and hope to find the deepest point. For unconstrained optimization, this is the only concept we need,but there are several design choices.

For constrained optimization, we need to introduce other concepts to manage the constraints.We will also introduce a special class of problems (convex optimization problems) where we can make statements about reaching the global optimum.

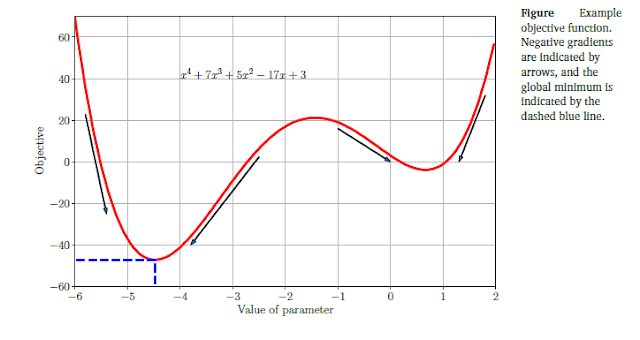
Consider the following function in Figure

The function has a global minimum around $x = -4.5$, with a function value of approximately $-47$. Since the function is “smooth,” the gradients can be used to help find the minimum by indicating whether we should take a step to the right or left.This assumes that we are in the correct bowl, as there exists another local minimum around $x = 0.7$. Recall that we can solve for all the stationary points of a function by calculating its derivative and setting it to zero. For

$f(x)=x^4+7x^3+5x^2-17x+3$

we obtain the corresponding gradient as

$\frac{\mathrm{d} f}{\mathrm{d} x}=4x^3+21x^2+10x-17$

Since this is a cubic equation, it has in general three solutions when set to zero. In the example, two of them are minimums and one is a maximum (around x = -1.4). To check whether a stationary point is a minimum or maximum, we need to take the derivative a second time and check whether the second derivative is positive or negative at the stationary point. In our case, the second derivative is

$\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}=12x^2+42x+10$

By substituting our visually estimated values of $x = -4.5;-1.4; 0.7;$ we will observe that as expected the middle point is a maximum $\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}<0$ and the other two stationary points are minimums.

Solving the problem analytically is complicated(According to the Abel–Ruffini theorem, there is in general no algebraic solution for polynomials of degree 5 or more Abel, 1826) and hence we need to start at some value, say $x_0 = -0.6$, and follow the negative gradient. The negative gradient indicates that we should go right, but not how far (this is called the step-size). Furthermore, if we had started at the right side (e.g., $x_0 = 0$) the negative gradient would have led us to the wrong minimum. Figure  illustrates the fact that for $x > -1$, the negative gradient points toward the minimum on the right of the figure, which has a larger objective value.

There is a class of functions called convex functions that do not exhibit this tricky dependency on the starting point of the optimization problem.For convex functions, all local minimums are global minimum. It turns out that many machine learning objective functions are designed such that they are convex.

The discussion  so far was about a one-dimensional function, where we are able to visualize the ideas of gradients, descent directions,and optimal values.We can develop the same ideas in high dimensions. Unfortunately, we can only visualize the concepts in one dimension.

Optimization using Gradient Descent

We now consider the problem of solving for the minimum of a real-valued function

$min _x  f(x) $

where $f : \mathbb{R}^d \to \mathbb{R}$ is an objective function that captures the machine learning problem at hand. We assume that our function $f$ is differentiable, and we are unable to analytically find a solution in closed form.

Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point.Note that the gradient points in the direction of the steepest ascent.Another useful intuition is to consider the set of lines where the function is at a certain value ($f(x) = c$ for some value $c\in \mathbb{R}$),which are known as the contour lines. The gradient points in a direction that is orthogonal to the contour lines of the function we wish to optimize.

Let us consider multivariate functions. Imagine a surface (described by the function $f(x)$ with a ball starting at a particular location $x_0$. When the ball is released, it will move downhill in the direction of steepest descent.Gradient descent exploits the fact that $f(x_0)$ decreases fastest if one moves from $x_0$ in the direction of the negative gradient $-((\bigtriangledown f)(x_0))^T$ of $f$ at $x_0$.

Then, if

$x_1 = x_0 - \gamma ((\bigtriangledown f)(x_0))^T$.

for a small step-size $\gamma  \ge 0$, then $f(x_1) \le f(x_0)$.

The simple gradient descent algorithm proceed as follows

If we want to find a local optimum $f(x_{*})$ of a function $f : \mathbb{R}^n \to \mathbb{R},\quad x \to f(x)$, we start with an initial guess $x_0$ of the parameters we wish to optimize and then iterate according to

$x_{i+1} = x_i - \gamma_i ((\bigtriangledown f)(x_i))^T \quad \cdots(1)$.

For suitable step-size  $\gamma_i$, the sequence $f(x_0) \ge f(x_1) \ge \cdots$ converges to a local minimum.

Consider the quadratic function in two dimensions 

$f\left(\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}\right)=\frac{1}{2}\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}^T\begin{bmatrix}
2 & 1\\
1& 20
\end{bmatrix}\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}-\begin{bmatrix}
5\\
3
\end{bmatrix}^T\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}$

with gradient

$\bigtriangledown f\left(\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}\right)=\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}^T\begin{bmatrix}
2 & 1\\
1& 20
\end{bmatrix}-\begin{bmatrix}
5\\
3
\end{bmatrix}^T$

Starting at the initial location $x_0=[-3,-1]^T$, we iteratively apply the eqn(1) to obtain a sequence of estimates that converges to the minimum value illustrated in above figure.We can see (both from the figure and by plugging $x_0$ into (1) with $\gamma = 0.085$) that the negative gradient at $x_0$ points north and east, leading to $x_1 = [-1.98, 1.21]^T$. Repeating that argument gives us $x_2 = [-1.32,-0.42]^T$, and so on.

Remark. Gradient descent can be relatively slow close to the minimum.Its asymptotic rate of convergence is inferior to many other methods. Using the ball rolling down the hill analogy, when the surface is a long, thin valley, the problem is poorly conditioned (Trefethen and Bau III, 1997).For poorly conditioned convex problems, gradient descent increasingly “zigzags” as the gradients point nearly orthogonally to the shortest direction to a minimum point

Step Size ( Learning Rate)

As mentioned earlier, choosing a good step-size is important in gradient descent. If the step-size is too small, gradient descent can be slow. If the The step-size is chosen too large, gradient descent can overshoot, fail to converge,or even diverge. We will discuss the use of momentum in the next section. It is a method that smooths out erratic behavior of gradient updates and dampens oscillations.

Adaptive gradient methods rescale the step-size at each iteration, depending on local properties of the function. There are two simple heuristics(Toussaint, 2012):

• When the function value increases after a gradient step, the step-size was too large. Undo the step and decrease the step-size.
• When the function value decreases the step could have been larger. Try to increase the step-size.

Although the “undo” step seems to be a waste of resources, using this heuristic guarantees monotonic convergence.

Example:Solving system of linear equation

When we solve linear equations of the form $Ax = b$, in practice we solve $Ax-b = 0$ approximately by finding $x$ that minimizes the squared error

$||Ax - b||^2 = (Ax - b)^T(Ax - b) $
if we use the Euclidean norm. The gradient  with respect to $x$ is
$\bigtriangledown x = 2(Ax - b)^TA$

We can use this gradient directly in a gradient descent algorithm. However,for this particular special case, it turns out that there is an analytic solution, which can be found by setting the gradient to zero

Remark. When applied to the solution of linear systems of equations $Ax =b$, gradient descent may converge slowly. The speed of convergence of gradient descent is dependent on the condition number 

$k = \frac{\sigma(A)_{max}}{\sigma(A)_{min}}$

 

which is the ratio of the maximum to the minimum singular value of $A$. The condition number essentially measures the ratio of the most curved direction versus the least curved direction, which corresponds to our imagery that poorly conditioned problems are long, thin valleys: They are very curved in one direction, but very flat in the other. Instead of directly solving $Ax = b$, one could instead solve $P^{-1}(Ax - b) = 0$, where $P$ is called the preconditioner. The goal is to design $P^{-1}$ such that $P^{-1}A$ has a better condition number, but at the same time $P^{-1}$ is easy to compute.

Example: (university question)

Consider the univariate function $f(x) = x^3 + 6x^2 - 3x - 5$

Find its stationary points and indicate whether they are maximum, minimum,or saddle points.

Given the function $f(x)$, we obtain the following gradient and Hessian,

$\frac{\mathrm{d} f}{\mathrm{d} x}=3x^2+12x-3$

$\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}=6x+12$

We find stationary points by setting the gradient to zero, and solving for $x$.

$3x^2+12x-3=0$

$x^2+4x-1=0$

$(x+2)^2-4-1=0$

$(x+2)^2=5$

$x=-2\pm \sqrt(5)$

Substituting the solutions of  $\frac{\mathrm{d} f}{\mathrm{d} x}$ into the Hessian gives

$\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}(-2+\sqrt{5}) \approx -13.4$ and

$\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}(-2-\sqrt{5}) \approx 13.4$ 

This means that the left stationary point is a maximum and the right one is a minimum.

Maximum and Minimum Values 

Let $f$ be a function of two variables $x$ and y. We say that $f$  has a local maximum at $(a, b)$ if $f(x, y) ≤ f(a, b)$ for all points $(x, y)$ in a neighborhood of $(a, b)$. We say that $f$ has a local minimum at $(a, b)$ if $f(x, y) ≥ f(a, b)$ for all points $(x, y)$ in a neighborhood of $(a, b)$.

If $f $ has a local extremum (that is, a local maximum or minimum) at $(a, b)$, and if the first order partial derivatives of $f$ exist there, then

$\frac{\mathrm{d} f}{\mathrm{d} x}(a,b)=0$ and

$\frac{\mathrm{d} f}{\mathrm{d} y}(a,b)=0$ 

Critical Points 

A point $(a, b)$ such that $∇f(a, b) = 0$, or one of the partial derivatives does not exist, is called a critical point of $f$. At a critical point, a function could have a local maximum, or a local minimum, or neither.If it is neither a maximum or minimum , it is called saddle point

The Second Derivative Test 

Let $f$ be a function of two variables $x$ and $y$. Suppose that all the second-order partial derivatives of $f$ are continuous in a neighborhood of $(a, b)$ and

$\frac{\mathrm{d} f}{\mathrm{d} x}(a,b)=0$ and

$\frac{\mathrm{d} f}{\mathrm{d} y}(a,b)=0$ 

Let 

$D=\begin{vmatrix}
fxx & fxy \\
fyx & fyy
\end{vmatrix}=fxxfyy-f^2xy$

We have the following results

(1) If $D(a, b) > 0$ and $fxx(a, b) > 0$, then $f(a, b)$ is a local minimum.
(2) If $D(a, b) > 0$ and $fxx(a, b) < 0$, then $f(a, b)$ is a local maximum.
(3) If $D(a, b) < 0$, then $(a, b)$ is a saddle point.
(4) If D(a, b) = 0, no conclusion may be drawn.

Example:
What are the extrema and saddle points of $f(x,y)=2x^3+xy^2+5x^2+y^2$

The theory to identify the extrema of $z=f(x,y)$ is:

Solve simultaneously the critical equations
$\frac{\mathrm{d} f}{\mathrm{d} x}=\frac{\mathrm{d} f}{\mathrm{d} y}=0$

Evaluate $fxx,fyy$ and $fxy(=fyx)$ at each of these critical points. 

Hence evaluate $D=fxxfyy−f^2xy$ at each of these points ( Determinant of Hessian)
Determine the nature of the extrema;

$D>0$ There is minimum if $fxx>0$ and a maximum if $fxx<0$
$D<0$ there is a saddle point
$D=0$ Further analysis is necessary
So we have:

$f(x,y)=2x^3+xy^2+5x^2+y^2$

Let us find the first partial derivatives:

$\frac{\mathrm{d} f}{\mathrm{d} x}=6x^2+y^2+10x$
$\frac{\mathrm{d} f}{\mathrm{d} y}=2xy+2y$

So our critical equations are:

$6x^2+y^2+10x=0$
$2xy+2y=0$

From the second equation we have:

$2y(x+1)=0⇒x=−1,y=0$

Subs $x=−1$ into the First equation and we get:

$6+y^2−10=0⇒y^2=4⇒y=±2$

Subs $y=0$ into the First equation and we get:

$6x^2+0^2+10x=0⇒2x(3x+5)=0⇒x=−5/3,0$

And so we have four critical points with coordinates;
$(−1,−2),(−1,2),(0,0),(−5/3,0)$

So, now let us look at the second partial derivatives so that we can determine the nature of the critical points:

$\frac{\mathrm{d}^2 f}{\mathrm{d} x^2} =12x+10$
$\frac{\mathrm{d}^2 f}{\mathrm{d} y^2} =2x+2$
$\frac{\mathrm{d}^2 f}{\mathrm{d} x \mathrm{d} y}=\frac{\mathrm{d}^2 f}{\mathrm{d}y \mathrm{d} x}=2y$

And we must calculate:

$D=\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}\frac{\mathrm{d}^2 f}{\mathrm{d} y^2}−\frac{\mathrm{d}^2 f}{\mathrm{d}x \mathrm{d}x}^2$

at each critical point. The second partial derivative values, $\$$D$  and conclusion are as follows:

$\begin{array}{cccccc}\text{Critical Point}& \frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial y^2}& \frac{{\partial }^{2}f}{\partial x\partial y}& & \text{Conclusion}\\ (0,0)& 10& 2& 0& >0& f_{xx}>0\Rightarrow \text{min}\\ (-1,-2)& -2& 0& 4& <0& \text{saddle}\\ (-1,2)& -2& 0& 4& <0& \text{saddle}\\ (-\frac{5}{3},0)& -10& -\frac{4}{3}& 0& >0& f_{xx}<0\Rightarrow \text{max}\end{array}$

Find the maximum and minimum values of the following function ( university question)

$f(x,y)=x^3+y^3-3x-12y+20$

Solve simultaneously the critical equations
$\frac{\mathrm{d} f}{\mathrm{d} x}=\frac{\mathrm{d} f}{\mathrm{d} y}=0$

Let us find the first partial derivatives:
$\frac{\mathrm{d} f}{\mathrm{d} x}=3x^2-3$
$\frac{\mathrm{d} f}{\mathrm{d} y}=3y^2-12$

So our critical equations are:
$3x^2-3=0$
$3y^2-12=0$

And so we have four critical points with coordinates;
$(1,2),(1,-2),(-1,2),(−1,-2)$

So, now let us look at the second partial derivatives so that we can determine the nature of the critical points:

$\frac{\mathrm{d}^2 f}{\mathrm{d} x^2} =6x$
$\frac{\mathrm{d}^2 f}{\mathrm{d} y^2} =6y$
$\frac{\mathrm{d}^2 f}{\mathrm{d} x \mathrm{d} y}=\frac{\mathrm{d}^2 f}{\mathrm{d}y \mathrm{d} x}=0$

And we must calculate:

$D=\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}\frac{\mathrm{d}^2 f}{\mathrm{d} y^2}−\frac{\mathrm{d}^2 f}{\mathrm{d}x \mathrm{d}x}^2$

at each critical point. The second partial derivative values, $D$  and conclusion are as follows:

Critical Point $\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}\quad \frac{\mathrm{d}^2 f}{\mathrm{d} y^2} \quad \frac{\mathrm{d}^2 f}{\mathrm{d} x \mathrm{d} y} \quad   D   \quad Conclusion$

(1,2)                   6        12              0        >0                $fxx>0$⇒min

(1,−2)                 6        -12            0         <0                saddle

(−1,2)               −6        12              0        <0                saddle

(−1,-2)              −6      −12             0        >0                $fxx<0$⇒max

So the minimum value of the function
$f(x,y)=x^3+y^3-3x-12y+20$

$f(1,2)=1+8-3-24+20=2$

The maximum value is

$f(x,y)=x^3+y^3-3x-12y+20$

$f(-1,-2)=-1-8+3+24+20=38$

Find the critical points of $f(x, y) = x^2 – 3xy+5x-2y+6y^2+8$

To find the  critical points compute the partial derivative and equate it to zero

$\frac{\partial f}{\partial x}=2x-3y+5=0$

$\frac{\partial f}{\partial y}=-3x-2+12y=0$

Solving these will get the critical point at $x=-18/5$ and $y=-11/15$

Find the extrema of the function $f(x,y)=x^2-y^2$ and categorize the same

$\frac{\partial f}{\partial x}=2x=0$

$\frac{\partial f}{\partial y}=-2y=0$

(0,0) is a criticl point

$\frac{\partial^2 f}{\partial x^2}=2$

$\frac{\partial^2 f}{\partial y^2}=-2$

$\frac{\mathrm{d}^2 f}{\mathrm{d} x \mathrm{d} y}=\frac{\mathrm{d}^2 f}{\mathrm{d}y \mathrm{d} x}=0$

$D=\frac{\mathrm{d}^2 f}{\mathrm{d} x^2}\frac{\mathrm{d}^2 f}{\mathrm{d} y^2}−\frac{\mathrm{d}^2 f}{\mathrm{d}x \mathrm{d}x}^2$

$D=-4-0=-4$ so it is a saddle point