Skip to main content

Difference between Batch Gradient Descent and Stochastic Gradient Descent



Gradient Descent
Gradient Descent is a generic optimization algorithm capable of finding optimal solutions to a wide range of problems.
The general idea is to tweak parameters iteratively in order to minimize the cost function.
An important parameter of Gradient Descent (GD) is the size of the steps, determined by the learning rate hyperparameters.
If the learning rate is too small, then the algorithm will have to go through many iterations to converge, which will take a long time, and if it is too high we may jump the optimal value.

Note: When using Gradient Descent, we should ensure that all features have a similar scale (e.g. using Scikit-Learn’s StandardScaler class), or else it will take much longer to converge.

Types of Gradient Descent:

Typically, there are three types of Gradient Descent: 
Batch Gradient Descent
Stochastic Gradient Descent
Mini-batch Gradient Descent

Stochastic Gradient Descent (SGD):

The word ‘stochastic‘ means a system or process linked with a random probability. Hence, in Stochastic Gradient Descent, a few samples are selected randomly instead of the whole data set for each iteration. In Gradient Descent, there is a term called “batch” which denotes the total number of samples from a dataset that is used for calculating the gradient for each iteration. In typical Gradient Descent optimization, like Batch Gradient Descent, the batch is taken to be the whole dataset. Although using the whole dataset is really useful for getting to the minima in a less noisy and less random manner, the problem arises when our dataset gets big.
Suppose, you have a million samples in your dataset, so if you use a typical Gradient Descent optimization technique, you will have to use all of the one million samples for completing one iteration while performing the Gradient Descent, and it has to be done for every iteration until the minima are reached. Hence, it becomes computationally very expensive to perform.
This problem is solved by Stochastic Gradient Descent. In SGD, it uses only a single sample, i.e., a batch size of one, to perform each iteration. The sample is randomly shuffled and selected for performing the iteration.
SGD algorithm:

So, in SGD, we find out the gradient of the cost function of a single example at each iteration instead of the sum of the gradient of the cost function of all the examples.

In SGD, since only one sample from the dataset is chosen at random for each iteration, the path taken by the algorithm to reach the minima is usually noisier than your typical Gradient Descent algorithm. But that doesn’t matter all that much because the path taken by the algorithm does not matter, as long as we reach the minima and with a significantly shorter training time.

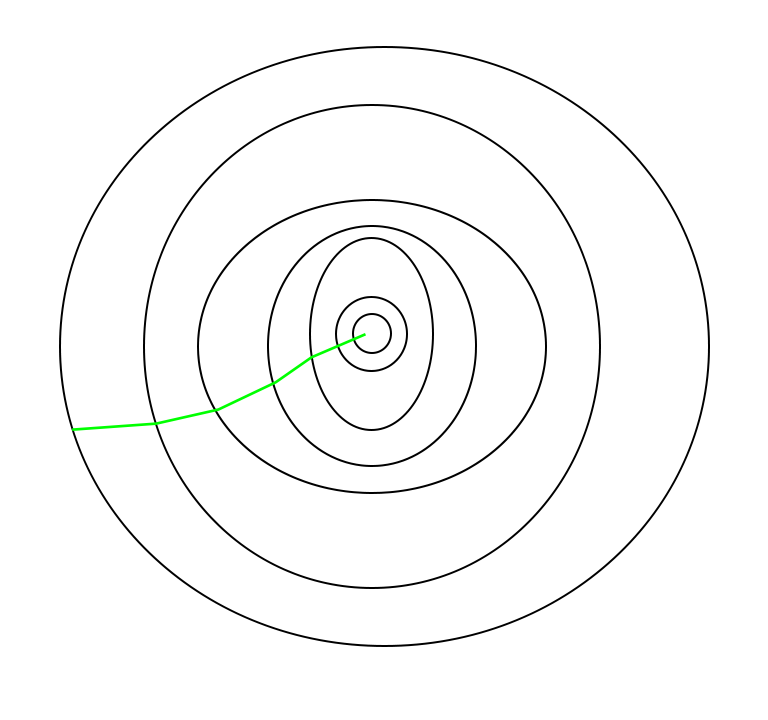
The path is taken by Batch Gradient Descent as shown below as follows:
gd_path

A path has been taken by Stochastic Gradient Descent –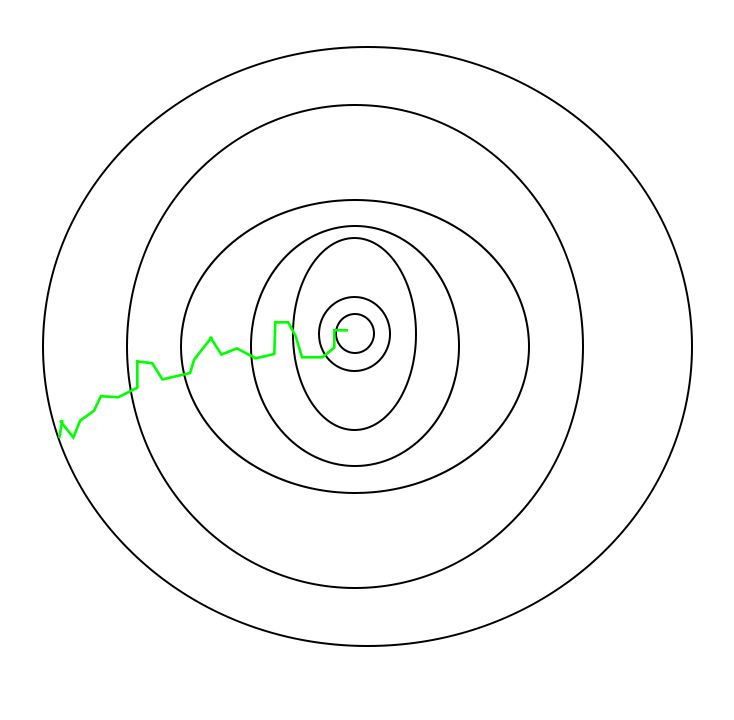

sgd_path

One thing to be noted is that, as SGD is generally noisier than typical Gradient Descent, it usually took a higher number of iterations to reach the minima, because of its randomness in its descent. Even though it requires a higher number of iterations to reach the minima than typical Gradient Descent, it is still computationally much less expensive than typical Gradient Descent. Hence, in most scenarios, SGD is preferred over Batch Gradient Descent for optimizing a learning algorithm.
S.NO.Batch Gradient DescentStochastic Gradient Descent
1.Computes gradient using the whole Training sampleComputes gradient using a single Training sample
2.Slow and computationally expensive algorithmFaster and less computationally expensive than Batch GD
3.Not suggested for huge training samples.Can be used for large training samples.
4.Deterministic in nature.Stochastic in nature.
5.Gives optimal solution given sufficient time to converge.Gives good solution but not optimal.
6.No random shuffling of points are required.The data sample should be in a random order, and this is why we want to shuffle the training set for every epoch.
7.Can’t escape shallow local minima easily.SGD can escape shallow local minima more easily.
8.Convergence is slow.Reaches the convergence much faster.    

Comments

Post a Comment

Popular posts from this blog

Mathematics for Machine Learning- CST 284 - KTU Minor Notes - Dr Binu V P

  Introduction About Me Syllabus Course Outcomes and Model Question Paper University Question Papers and Evaluation Scheme -Mathematics for Machine learning CST 284 KTU Overview of Machine Learning What is Machine Learning (video) Learn the Seven Steps in Machine Learning (video) Linear Algebra in Machine Learning Module I- Linear Algebra 1.Geometry of Linear Equations (video-Gilbert Strang) 2.Elimination with Matrices (video-Gilbert Strang) 3.Solving System of equations using Gauss Elimination Method 4.Row Echelon form and Reduced Row Echelon Form -Python Code 5.Solving system of equations Python code 6. Practice problems Gauss Elimination ( contact) 7.Finding Inverse using Gauss Jordan Elimination  (video) 8.Finding Inverse using Gauss Jordan Elimination-Python code Vectors in Machine Learning- Basics 9.Vector spaces and sub spaces 10.Linear Independence 11.Linear Independence, Basis and Dimension (video) 12.Generating set basis and span 13.Rank of a Matrix 14.Linear Mapping...
Post a Comment
Read more

Vectors in Machine Learning

As data scientists we work with data in various formats such as text images and numerical values We often use vectors to represent data in a structured and efficient manner especially in machine learning applications In this blog post we will explore what vectors are in terms of machine learning their significance and how they are used What is a Vector? In mathematics, a vector is a mathematical object that has both magnitude and direction. In machine learning, a vector is a mathematical representation of a set of numerical values. Vectors are usually represented as arrays or lists of numbers, and each number in the list represents a specific feature or attribute of the data. For example, suppose we have a dataset of houses, and we want to predict their prices based on their features such as the number of bedrooms, the size of the house, and the location. We can represent each house as a vector, where each element of the vector represents a specific feature of the house, such as the nu...
Post a Comment
Read more

2.14 Singular Value Decomposition

The Singular Value Decomposition ( SVD) of a matrix is a central matrix decomposition method in linear algebra.It can be applied to all matrices,not only to square matrices and it always exists.It has been referred to as the 'fundamental theorem of linear algebra'( strang 1993). SVD Theorem: Let $A^{m \times n}$ be a rectangular matrix of rank $r \in [0,min(m,n)]$. The SVD of A is a decomposition of the form. $A= U \Sigma V^T $ with an orthogonal matrix $U \in \mathbb{R}^{m \times m}$ with column vectors $u_i, i=1,\ldots,m$ and an orthogonal matrix $V \in \mathbb{R}^{n \times n}$ with column vectors $v_j, j=1,\ldots,n$.Moreover, $\Sigma$ is an $m \times n$ matrix with $\sum_{ii} = \sigma \ge 0$ and $\sigma_{ij}=0, i \ne j$. The diagonal entries $\Sigma_i=1,\ldots,r$ of $\sigma$ are called singular values . $u_i$ are called left singular vectors , and $v_j$ are called right singular vectors .By convention singular values are ordered ie; $\sigma_1 \ge \sigma_2 \ldots \sigma_r \...
Post a Comment
Read more